What is Information?
Kyle Geske
Table of Contents
- The Paper
- Christoph Adami
- Information
- What Is Information?
- What Is Information?
- Predictions of What?
- Predictions of What?
- Better than Chance?
- Probability
- Dicing
- Uncertaintly
- The Log of States
- Logarithms
- Logarithmic Bases
- Asking Questions
- Asking Questions
- Encoding Entropy
- The Eye of the Beholder
- The Eye of the Beholder
- Entropy is Subjective
- What Does it Mean to Have Information
- Card Tricks
- Pick a Card!
- Gaining Information
- The Weather Device
- Weather Communication
- Weather Communication
- Compressing Entropy
- Different Entropies
- Conditional Probability
- Everything is Conditional
- Conditional Crashing
- What is Information?
- Let's Recap...
- Let's Recap
- Units of Measurement
- Applications of Information Theory
- The Information Theory of Life
- Thank You Kindly
The Paper
Title: What is Information?
Author: Christoph Adami
Published: Philosophical Transactions of the Royal Society A, 2016
TL;DR: Information is what you don’t know minus what remains to be known given what you know.
If there are errors in this presentation they should be attributed to my lack of understanding of the paper, not to the paper itself.
Christoph Adami

Christoph Adami is a computational biologist with a focus on theoretical, experimental and computational Darwinian evolution.
A professor of Microbiology and Molecular Genetics as well as Physics and Astronomy at Michigan State University, he uses mathematics and computation to understand how simple rules can give rise to the most complex systems and behaviours.
Many of my slides contain direct quotes from Mr Adami’s paper.
Resources
Information
Information is central to our daily lives.
We rely on information to make sense of the world, to make informed decisions.
What Is Information?
Information is that which allows you* to make predictions with accuracy better than chance.
*You, who possesses the information.
What Is Information?
Information is that which allows you to make predictions with accuracy better than chance.
Okay, but:
- Predictions about what?
- What exactly is “better than chance”?
Predictions of What?
Predictions of other systems.
Entropy is how much we don’t know about the other system.
Information can be rigorously defined in terms of entropy.
Predictions of What?

Predictions of the states the system can take on. :)
Coin, 2 states
- heads
- tails
Standard Die, 6 states
- 1 through 6 dots
Weather Condition, 47 on Yahoo Weather
- sunny
- cloudy
- rainy
- snowy
- etc.
Better than Chance?

Probability is the study of chance.
The study of things that might happen or might not happen.
Probability

The probability (p) of an event is always between zero (impossible) and one (certain).
The sum of the probabilities of possible events is always 1.
Flipping a fair coin has two possible outcome events:
- Heads, with a probability of ph
- Tails, with a probability of pt
p = p(h) + p(t) = 0.5 + 0.5 = 1
Resources
Dicing

When rolling a die, the probability of landing on any given side is 1/N.
N being the number of side of the dice.
When rolling a fair six-sided die, each side has a probability of 1/6.
When rolling a fair four-sided die, each side has a probability of 1/4.
Resources
Uncertaintly

How much don’t we know before a coin flip?
Is it two?
How much don’t we know before the role of a 4 sided die?
Is it four?
What are the entropies of these systems?
The Log of States
No, the uncertainty (or entropy) of an event isn’t equal the number of possible states.
It’s better quantified as the logarithm of the number of states.
The uncertainty of a coin flip isn’t 2, it’s log(2).
The uncertainty of a 4-sided die roll isn’t 4, it’s log(4).
But why?
Logarithms
From the Greek logos meaning proportion or ratio and arithmos meaning number.
A logarithm is a ratio number, a measure of proportional scale.
The Richter scale measures earthquake intensity on a base-10 logarithmic scale. An 8.2 quake on the Richter scale is 10 times larger than an 7.2, 100 times larger than a 6.2, 1000 times larger than a 5.2, etc.
The pH scale for the acidity of a water-soluble substance is also a base-10 logarithmic scale. High numbers are bases, low numbers are acids. Vinegar, with a pH of around 2 is 1000 times more acidic than coffee, which has a pH of around 5.
Resources
Logarithms, Explained (video)
Logarithmic Bases
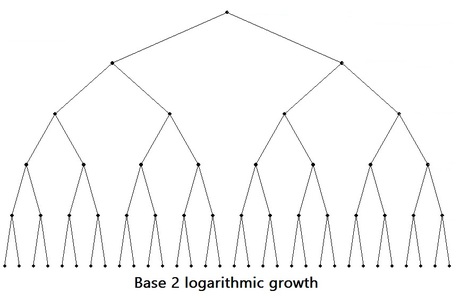
Logarithmic scales show orders of magnitude, but they don’t always have to be orders of 10.
The logarithmic base raised to what power equals the number?
bp = n
logbn = p
| log10 | log2 |
|---|---|
| log101 = 0 | log21 = 0 |
| log1010 = 1 | log22 = 1 |
| log10100 = 2 | log24 = 2 |
| log101000 = 3 | log28 = 3 |
Asking Questions

So why is the uncertainty of a coin flip, log(2)?
When we’re uncertain about something we ask questions!
For base 2 logs, the uncertainty of a system can defined as:
The number of yes/no questions we have to ask to determine the outcome of a system.
Asking Questions

For a coin flip with two states, the entropy is log(2) = 1 bit.
We only need to ask one question to determine the outcome:
- Is it heads?
What about for a four sided die? An eight sided die?
Entropy is logarithmic because decision trees grow logarithmically.
Encoding Entropy
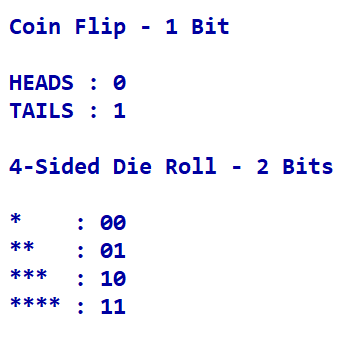
Another way to look at entropy is in terms of encoding or transcribing possible outcomes.
How many bits are required to communicate the outcome of a coin flip?
How about for a 4-sided die?
The Eye of the Beholder

So, what is the entropy of a coin? Is it log(2)?
What if I told you it was infinite?
If a coin has only two sides how can its entropy be infinite?
Well, because entropy is subjective. It depends on what we care about, what we choose to measure.
The Eye of the Beholder
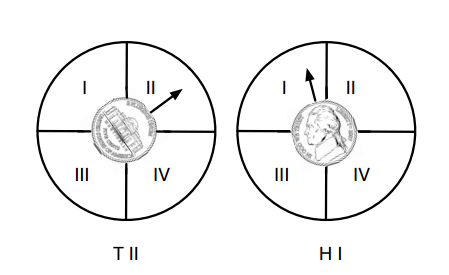
“What if I told you that I’m playing a somewhat different game, one where I’m not just counting whether the coin comes up heads or tails, but am also counting the angle that the face has made with a line that points towards True North. And in my game, I allow four different quadrants”
There are now 8 states. (2 sides times 4 quadrants)
So is the entropy now log(8)? Sure, until I change the game!
Entropy is Subjective
The entropy of a physical object is not defined unless you tell me which degrees of freedom are important to you.
In other words, it is defined by the number of states that can be resolved by the measurement that you are going to be using to determine the state of the physical object.
In this way uncertainty is infinite, made finite only by the finiteness of our measurement devices.
What Does it Mean to Have Information

Imagine a urn filled with coloured balls…
Wait, what?
Let’s take two examples in instead:
- Gaining information about a card selected at random.
- Gaining information about a weather system.
Card Tricks
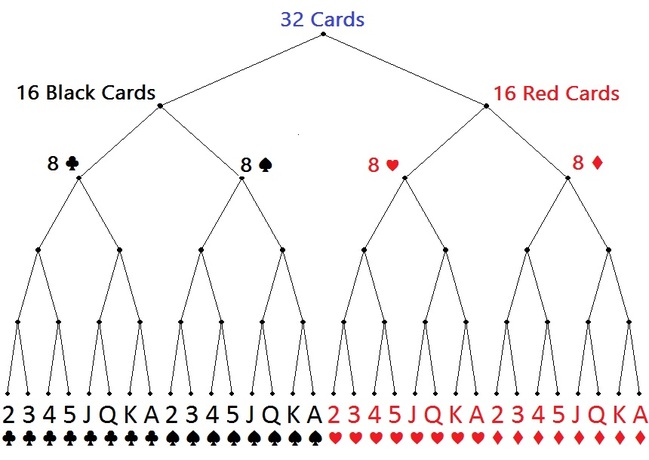
Imagine a deck of 32 cards: Two colours, four suits, 8 cards of each suit.
Pick a Card!
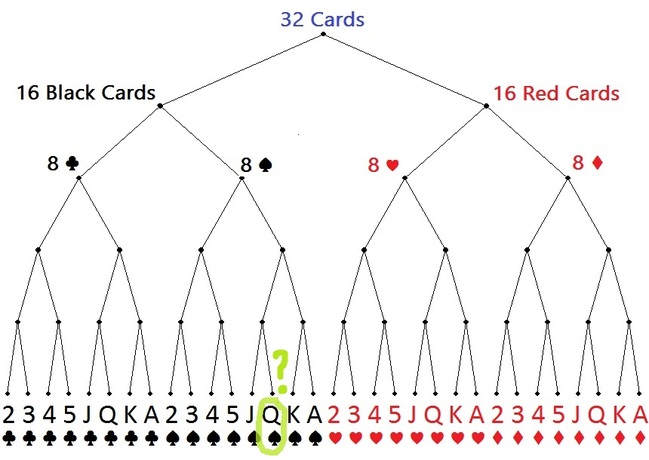
When picking a random card from the deck, what’s the chance it’s the Queen of spades?
The probability is 1/32. The uncertainty is log232, or 5 bits.
It would take 5 bits to describe all the equally possible outcomes.
Said another way, I would need to ask 5 questions to determine the outcome of a randomly selected card.
Gaining Information
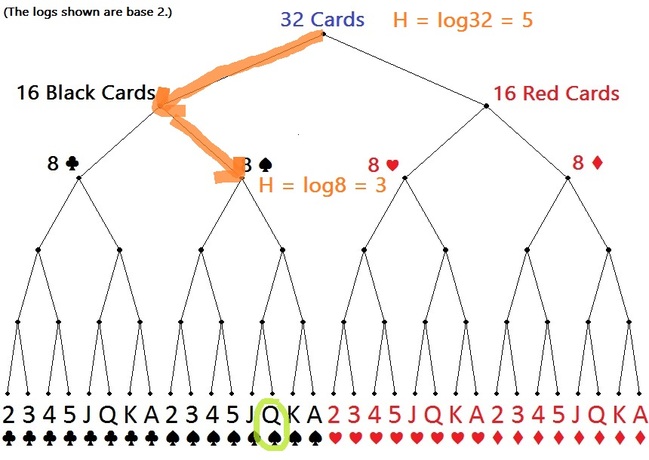
If I told you the card selected is a spade, then the probability that it’s the Queen of Spades goes from 1/32 to 1/8. You’ve gained two bits of information!
Resources
- What is Information Entropy? - “Art of the Problem” Video
The Weather Device

Let’s think about quantifying information in terms of binary communication.
Imagine we have a weather measurement device. It’s a crude device that lumps all weather into four categories:
- Sunny
- Cloudy
- Rainy
- Snowy
Weather Communication
Let’s assume I need to communicate the weather of a city using a simple code with only two symbols.
When I know nothing about the weather, other than its possible states, I need two bits to communicate the weather:
Sunny = 00
Cloudy = 01
Rainy = 10
Snowy = 11
In other words, the system has two bits of entropy.
Weather Communication
Let’s imagine I’m using this device to communicate the weather every day for years.
I’m also collecting stats on the different states.
I notice that on average:
- it’s sunny 1/2 of the time
- it’s cloudy 1/4 of the time
- it’s rainy 1/8 of the time
- it’s snowing 1/8 of the time
Compressing Entropy
Given what I know about the probable states of the weather I can devise a new code:
Sunny = 0
Cloudy = 10
Rainy = 110
Snowy = 111
In the long run we need fewer than 2 bits to communicate the weather!
What allows us to compress our communications is our understanding of the probabilities of the states.
psun = 1/2
pcloud = 1/4
prain = 1/8
psnow = 1/8
H = (1/2 * 1 bit ) + (1/4 * 2 bits) + (1/8 * 3 bits) + (1/8 * 3 bits)
H = 0.5 + 0.5 + 0.375 + 0.375 = 1.75 bits
H = (psun * log(1/psun))
+ (pcloud * log(1/pcloud))
+ (prain * log(1/prain))
+ (psnow * log(1/psnow))
H = (psun * -log(psun))
+ (pcloud * -log(pcloud))
+ (prain * -log(prain))
+ (psnow * -log(psnow))
Resources
Different Entropies
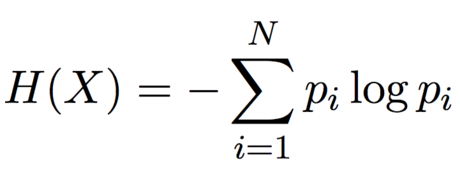
Entropy is maximum when all we know is the number of states:
Hmax = log(N)
When we know the probabilities of the states we get a different entropy H(X).
Information is the delta, the difference between these entropies.
I = Hmax - H(X)
Conditional Probability
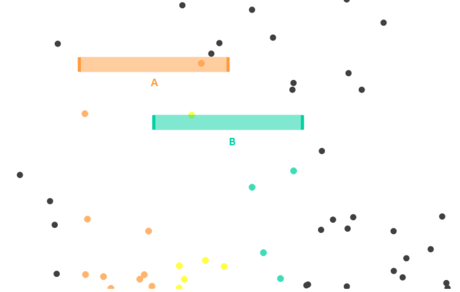
A conditional probability is the probability of an event, given some other event has already occurred.
P(A) = Probability of a ball hitting shelf A
P(B) = Probability of a ball hitting shelf B
P(A|B) = Probability of a ball hitting shelf A given we know that it hit shelf B.
P(A) = 1/3
P(B) = 1/3
P(A|B) = 1/2
Everything is Conditional
The ability to make better than chance predictions about a system is always conditional on some knowledge.
That knowledge is gained information.
In our card example our gain of information was conditional on pruning the number of possible outcomes.
In our weather example our gain of information was conditional on learning the probabilities of the weather outcomes through experimentation.
Everything is conditional!
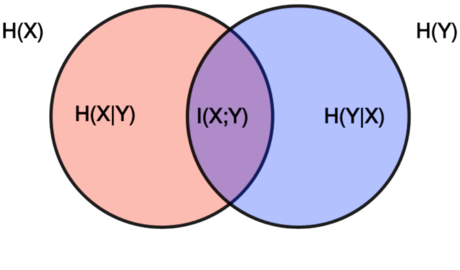
Conditional Crashing
| Manoeuvre | Car Crash | Texting |
|---|---|---|
| forward | no | yes |
| right turn | no | no |
| right turn | yes | yes |
| left turn | no | yes |
| reverse | no | no |
| left turn | no | no |
| reverse | yes | yes |
| forward | no | no |
| ... | ... | ... |
X = Crashing While Driving
H(X) = Uncertainty of Crashing while Driving
WHAT YOU DON'T KNOW about Crashing while driving.
Y = Driving While Texting
H(Y) = Uncertainty of Driving while Texting
H(X|Y) = Uncertainty of Crashing while Driving, Given Texting Status
WHAT REMAINS TO BE KNOWN about Crashing while Driving
GIVEN WHAT YOU KNOW about Driving while Texting.
I(X:Y) = Information Gained About Crashing While Driving
Shared Entropy. Mutual Information.
I(X:Y) = H(X) - H(X|Y)
WHAT YOU DON'T KNOW
minus
WHAT REMAINS TO BE KNOWN GIVEN WHAT YOU KNOWWhat is Information?
Information is what you don’t know minus what remains to be known given what you know.
And we’ve defined two types of information:
I = Hmax - H(X)
I = H(X) - H(X|Y)
If we add those together we get:
Itotal = Hmax - H(X) + H(X) - H(X|Y)
Itotal = Hmax - H(X|Y)
Let's Recap...
Information and entropy are different things.
Entropy is a word we use to quantify how much isn’t known about a system.
We can know more about a system by performing experiments and making measurements.
The difference in entropies (for example before and after a measurement) is what we call information.
Let's Recap
Probability distributions are born being uniform.
These probability distributions become non-uniform once you acquire information about the states.
This information is manifested by conditional probabilities.
Units of Measurement
The base of the log gives you the units for measuring entropy.
Information Units:
- Log base 2: a bit (or a shannon)
- Log base 3: a trit
- Log base 10: a dit, (a hartley, hart, or ban)
- Log base e: a nat (or natural)
Applications of Information Theory
Christoph Adami has been applying information theory to research on:
The Information Theory of Life
“Information is the currency of life. One definition of information is the ability to make predictions with a likelihood better than chance. That’s what any living organism needs to be able to do, because if you can do that, you’re surviving at a higher rate. Lower organisms make predictions that there’s carbon, water and sugar. Higher organisms make predictions about, for example, whether an organism is after you and you want to escape. Our DNA is an encyclopedia about the world we live in and how to survive in it.
Think of evolution as a process where information is flowing from the environment into the genome. The genome learns more about the environment, and with this information, the genome can make predictions about the state of the environment.
The secret of all life is that through the copying process, we take something that is extraordinarily rare and make it extraordinarily abundant.” - Christoph Adami
Thank You Kindly
Questions?