On Computable Numbers, with an Application to Entscheidungsproblem
Kyle Geske
Table of Contents
- The Paper
- Computable Numbers
- Entscheidungsproblem
- Mr. Turing Needs a Machine
- Human Computation
- State Machines
- Turnstile State Machine Analogy
- Turnstile State Machine
- Adding a Tape
- Turing Machines
- Examples of Turing Machine
- Binary Counter Machine
- Circular or Circle-Free Machines
- Encoding Turing Machines
- The Universal Turing Machine
- Limits of Computation
- References and Further Reading
The Paper

Title: On Computable Numbers,
with an Application to Entscheidungsproblem
Author: Alan Turing
Published: Journal of Math, Volume 58, 1936
TL;DR: Turing invents a programmable machine to show the power of computation and to expose the limits of formal mathematical systems.
Resources
Computable Numbers

“The real numbers whose expressions as a decimal are calculable by finite means. ”
“A number is computable if its decimal can be written down by a machine.”
Turing’s computable numbers will be binary numbers in the range 0 to 1.
For example, 1/3 in binary is:
0.0101010101010101...
How is 1/3 equal to 0.0101010101010101… in binary?
1/3 = 0.0101010101010101...
1/3 = (0 * 2^-1) + (1 * 2^-2) + (0 * 2^-3) + (1 + * 2^-4) + ...
1/3 = 1/4 + 1/16 + 1/64 + 1/256 + ...
Resources
Entscheidungsproblem

Pronounced: Ent-shy-dungs-prob-lem
Entscheidungs is a German word for decision/decidability.
Hilbert’s Ideal Formal Mathematical System
- Consistent - No contradictory well-formed formula.
- Complete - All true formulas can be derived from the axioms.
- Decidable - Finite decision procedure exists to determine provability of any given well-formed formula.
The Entscheidungsproblem or decision problem involves finding the procedure mentioned in item three of this list.
Resources
Mr. Turing Needs a Machine
Heinrich Behmann on the Entscheidungsproblem:
“It is of fundamental importance for the character of this problem that only mechanical calculations according to given instructions, without any thought activity in the stricter sense, are admitted as tools for the proof. One could, if one wanted to, speak of mechanical or machinelike thought.
Perhaps one could later let the procedure be carried out by a machine.”
For Turing to show the Entscheidungsproblem unsolvable he first needs to invent such a machine.
Human Computation

Turing first investigates how humans work through calculations.
When performing a computation the human has:
- A finite number of symbols with which to work.
- Discrete states of mind they can switch between.
- A paper on which to perform calculations and record results.
Resources
State Machines
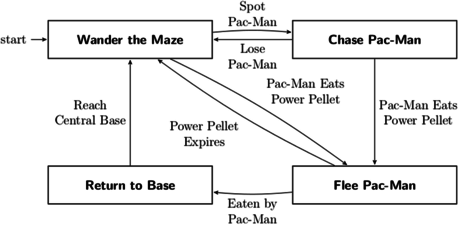
An abstract machine that can be in one of a finite number of states.
The machine is in only one state at a time, its current state.
It can transition from one state to another when initiated by a triggering event.
Resources
Turnstile State Machine Analogy

A turnstile is a type of one-way gate.
Locked until payment is made.
Payment unlocks for a single person.
Resources
Turnstile State Machine
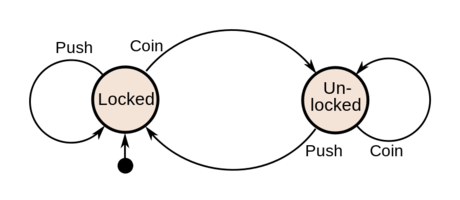
A one-way turnstile used for subways modeled as a state machine.
| Current State | Input | Next State | Output |
|---|---|---|---|
| Locked | coin | Unlocked | Unlock turnstile so customer can push through. |
| push | Locked | None | |
| Unlocked | coin | Unlocked | None |
| push | Locked | When customer has pushed through, lock turnstile. |
Resources
Adding a Tape
Turing’s machines are state machines with the ability to read from and write to a tape.
The tape is divided into squares each capable of bearing a symbol.
The tape is of infinite length.
Resources
Turing Machines

State Machine + Tape = Simplest Computer
The machine state combined with the currently scanner symbol is called the configuration.
A configuration may lead to:
- A change in the state
- Writing a symbol to a blank square
- Erasing a symbol from a square
- Moving the tape by one square in either direction
Resources
Examples of Turing Machine
Turing machine for printing out the binary form of 1/3:
| Configuration | Behaviour | |||
|---|---|---|---|---|
| State | Symbol | Move | Next State | |
| a | blank | Print 0 | Move R | b |
| b | blank | Print 1 | Move R | a |
Binary Counter Machine
Turing machine implementing a binary counter:
| Configuration | Behaviour | |||
|---|---|---|---|---|
| State | Symbol | Move | Next State | |
| begin | blank | Print 0 | increment | |
| increment | blank | Print 1 | rewind | |
| increment | 0 | Print 1 | rewind | |
| increment | 1 | Print 0 | Move L | increment |
| rewind | blank | Move L | increment | |
| rewind | 0 | Move R | rewind | |
| rewind | 1 | Move R | rewind | |
Circular or Circle-Free Machines
Once set in motion a Turing machine will write an infinite number of figures to it’s tape.
A circular machine is one that eventually stops writing figures.
A non-circular machine is said to be circle-free.
* * *
Both types of machines will run for an infinite length of time, the difference is their output.
A circle-free machine produces results forever, while a circular machine will eventually get stuck in a non-productive loop.
Resources
Encoding Turing Machines
Turing Machines can be described as quintuples q s q' s' d separated by semicolons.
qis the current statesis the symbol currently under the read/write headq'is the next state to enters'is the symbol to be written in place ofsdis the direction the tape head should move
A descriptions of the 1/3 machine could be written as:
a _ b 0 R ; b _ a 1 R
The complete configuration of a machine is its current state and its current tape.
Snapshots of the complete configuration of the 1/3 machine separated by colons:
a:b0:0a1:01b0:010a1:0101b0:01010a1:...
The state is recorded directly in front of the current tape read/write position.
The Universal Turing Machine

Given that we can capture as a string of symbols:
- Any Turing machine description.
- The state and tape of a Turing machine at any point in time.
We can build a Turing machine U that can take as input from its tape the description of any other Turing machine M.
This machine U will output successive snapshots of the state and tape of M.
In the paper, Turing describes how to build this machine-simulating machine, which he calls a universal machine.
Resources
Limits of Computation

1. An Uncomputable Number
A number that can be described but not computed.
2. An Impossible Machine
The Halting Problem cannot be solved.
3. Entscheidungsproblem
A halting problem hides within first order predicate logic.
References and Further Reading

The New Turing Omnibus - A. K. Dewdney 66 Excursions in Computer Science
The Annotated Turing - Charles Petzold
A Guided Tour through Alan Turing’s Historic Paper on Computability and the Turing Machine
Cryptonomicon - Neal Stephenson
A novel about WWII cryptography and modern-day data havens with Turing as one of the characters.
Gödel, Escher, Bach - Douglas Hofstadter
An Eternal Golden Braid
Resources
The Paper: On Computable Numbers, with an application to the Entscheidungsproblem - Alan Turing